猪脚说第五期

在这一部分中，我们会针对同学们问的比较多的题目（或者易错点较多的题目），给出若干的代码。大家可以参考题解中的代码，学习一下代码规范【好好看看哪里要空格哪里要空行！！！】，对比一下自己的代码与我们给出的参考代码，孰优孰劣,亦或者代码中的某些段落可以打包成一个固定模版，在后续作业、考试中使用。

如果针对这些题，同学们有更好更简洁的方法，欢迎来找助教讨论分享，助教请喝奶茶。

表达式计算（支持空格，连乘，连除）

法一：先计算乘除，再加减（先计算表达式中所有的乘除，再从左到右进行加减）。

#include <stdio.h>
#include <string.h>

int main() 
{
    char a[512] = {0}, b[512] = {0}, op[512] = {0};
    int len, i,j = 0, k = 0, cnt;
    long long ans, num[512] = {0}; 
    	// 虽然数字都是int型，但int型的数字相加和相乘可能超int范围
    
    gets(a);
    len = strlen(a);
    
    for (i = 0; i < len; i++) {
        if(a[i] != ' ')
            b[k++] = a[i];
    } // 将清除空格后的字符串保存在数组b中
    
    for (i = 0; b[i] != '\0'; i++) {
        if (b[i] >= '0' && b[i] <= '9')
            num[j] = 10 * num[j] + b[i] - '0'; // 非常好用的从一串字符中读取整数数字的方法
        else {
            op[j] = b[i];
            j++;
        }
    } // 将数字与运算符分别存进两个数组，一个数字对应一个运算符，下标一一对应
    
    cnt = j;
    
    for (i = 0; i < cnt; i++) {
        if (op[i] == '*'){
            num[i] = num[i] * num[i + 1];
            for (j = i; j < cnt - 1; j++)
                op[j] = op[j + 1];
            for (j = i + 1; j < cnt - 1; j++)
                num[j] = num[j + 1];
            i--;
            cnt--;
        }
        // 若遇到*，则计算当前两个数的乘积，保存到*前的数，后面的数与运算符往前移。
        // 由于前移了，则下次进入循环时仍然该从当前位开始，为了抵消i++的影响，执行
        // 一次i--，同时总数cnt--
        else if (op[i] == '/') {
            num[i] = num[i] / num[i + 1];
            for (j = i; j < cnt - 1; j++)
                op[j] = op[j + 1];
            for (j = i + 1; j < cnt - 1; j++)
                num[j] = num[j + 1];
            i--;
            cnt--;
        }
    }
    
    ans = num[0]; // 此时表达式中的乘除已全部处理完毕，接下来从左到右执行加减运算即可。
    for (i = 0; i < cnt; i++) {
        if (op[i] == '+')
            ans += num[i + 1];
        else if (op[i] == '-')
            ans -= num[i + 1];
    }
    
    printf("%lld\n", ans);
    
    return 0;
}

法二：后悔法（读入什么就运算什么，读到乘除往前反悔）。

#include <stdio.h>
#include <string.h>

int main() 
{
    char s[512] = {0}, x[512] = {0}, t[512] = {0}, a[512] = {0};
    int i, j = 0, k = 0, k1 = 1, len, len1, ans = 0;
    
    gets(s);
    len = strlen(s);
    for (i = 0; i < len; i++) {
        if(s[i] != ' ')
            x[k++] = s[i];
    } // 将清除空格后的字符串保存在数组x中
    
    len1 = strlen(x);
    for (i = 0; i < len1 - 1; i++) {
        if(x[i] >= '0' && x[i] <= '9')
            a[j] = 10 * a[j] + x[i] - '0'; // 非常好用的从一串字符中读取整数数字的方法
        else {
            t[j] = x[i];
            j++;
        } // 将数字与运算符分别存进两个数组，一个数字对应一个运算符，下标一一对应
    }     // 不需要考虑末尾的“=”，因此循环结束条件为i<len1-1
    
    ans += a[0]; // 记录第一个数字为当前运算结果
    for (i = 0; i < j; i++) {
        if (t[i] == '*') {
            if(i == 0) {
                ans = ans - a[i] + a[i] * a[i + 1];
                a[i + 1] = a[i] * a[i + 1];
            } // 特判，第一个符号为乘号
            else {
                if (t[i - k1] == '+'){
                    ans = ans - a[i] + a[i] * a[i + 1];
                    // 1+2*3，先算1+2得到3，读到*后，往前反悔，
                    // 于是当前预算结果为3-2+2*3，后续思路相同
                    a[i + 1] = a[i] * a[i + 1];
                    k1++;
                    // 对于连乘，1+2*3*4，运算到1+2*3为7时，再读到乘号，需要用变量k1记录
                    // 连续乘or除多少次，反悔时才能找到相应位置，于是现在运算结果为7-6+6*4，
                    // 后续思路相同
                }
                else if (t[i - k1] == '-') {
                    ans = ans + a[i] - a[i] * a[i + 1];
                    a[i + 1] = a[i] * a[i + 1];
                    k1++;
                }
                else if (t[i - k1] == '*') {
                    ans *= a[i + 1];
                    k1++;
                }
                else if (t[i - k1] == '/') {
                    ans *= a[i + 1];
                    k1++;
                }
            }
        }
        else if (t[i] == '/') {
            if (i == 0) {
                ans = ans - a[i] + a[i] / a[i + 1];
                a[i + 1] = a[i] / a[i + 1];
            }
            else {
                if (t[i-k1] == '+') {
                    ans = ans - a[i] + a[i] / a[i + 1];
                    a[i + 1] = a[i] / a[i + 1];
                    k1++;
                }
                else if (t[i - k1] == '-') {
                    ans = ans + a[i] - a[i] / a[i + 1];
                    a[i + 1] = a[i] / a[i + 1];
                    k1++;
                }
                else if (t[i - k1] == '*') {
                    ans /= a[i + 1];
                    k1++;
                }
                else if (t[i - k1] == '/') {
                    ans /= a[i + 1];
                    k1++;
                }
            }
        }
        else if (t[i] == '+') {
            ans += a[i + 1];
            k1 = 1;
        }
        else if (t[i] == '-') {
            ans -= a[i + 1];
            k1 = 1;
        }
    }
    
    printf("%d\n", ans);
    
    return 0;
}

法三：使用scanf函数可以自动消除空格，同时每次将一个数字和一个运算符成对读入，直接进行运算。

#include <stdio.h>

int main()
{
    int num1 = 0, num2, num3;
    char op1 = '+', op2, op3; // 这样初始化是为了输入第一个数num2时，可以实现0+num2的效果
    
    while(1) {
        scanf("%d %c",&num2, &op2);
        
        while (op2 == '*' || op2 == '/') { 
            // 当输出乘除时，继续往后输入，直到退出连乘/除为止
            scanf("%d %c", &num3, &op3);
            if (op2 == '*')
                num2 = num2 * num3;
            else
                num2 = num2 / num3;
            op2 = op3; // 更新op2为当前输入的符号
        } // 此时已经退出连乘/除模式，往后直接执行加减操作
        
        if (op1 == '+')
            num1 = num1 + num2;
        else if (op1 == '-')
            num1 = num1 - num2;
        
        op1 = op2; // 更新op1为当前当前输入的符号
        
        if (op1 == '=') {
            printf("%d\n", num1);
            break;
        }
    }
    return 0 ;
}

超长正整数的减法

这道题的易错点在于：

1、连续借位相减（例如执行 10000 - 1 的运算）；

2、有些同学使用长度和字典序关系判断两数大小，这是正确且高效的方法，但请注意strcmp()函数的返回值；

3、注意0和'0'的区别，对其他数字也是同理。

#include <stdio.h>
#include <string.h>

#define M 1000

int main()
{
    char str_a[M] = {0}, str_b[M] ={ 0};
    int num_a[M] = {0}, num_b[M] = {0}, num_c[M] = {0};
    int len_a, len_b;
    int i, j, k, n, f = 0;
    
    gets(str_a);
    gets(str_b);
    len_a = strlen(str_a);
    len_b = strlen(str_b);
    
    if (len_a < len_b)
        k = len_b;
    else
        k = len_a; // 让k为两数组的最大长度
    
    if (len_a > len_b)
        n = 1;
    else if (len_a == len_b)
        n = strcmp(str_a, str_b) >= 0 ? 1 : -1;
    else
        n = -1; //给n赋值，在之后判断需不需要打印负号
    
    for (i = len_a - 1, j = 0; i >= 0; i--, j++)
        num_a[j] = str_a[i] - '0'; 
    // 很经典的将字符'0'转换成数字0的方法，且同时实现数组反序存储
    
    for (i = len_b - 1, j = 0; i >= 0; i--, j++)
        num_b[j] = str_b[i] - '0';
    
    for (i = 0; i < k; i++) {
        if (n >= 0) { // 判断n是为了让程序永远执行大数减小数
            if (num_a[i] - num_b[i] >= 0)
                num_c[i] = num_a[i] - num_b[i];
            else {
                num_c[i] = num_a[i] + 10 - num_b[i];
                num_a[i+1]--;
            } // 借位的判断
        }
        else {
            if (num_b[i] - num_a[i] >= 0)
                num_c[i] = num_b[i] - num_a[i];
            else {
                num_c[i] = num_b[i] + 10 - num_a[i];
                num_b[i + 1]--;
            }
        }
    }
    
    if (n < 0)
        printf("-");
    for (i = k - 1; i >= 0; i--) {
        if (num_c[i])
            f = 1;
            // 只要num_c数组中不是0，则把f赋值为1，目的只是为了消除
            // 打印出的数组中的前导0，所以不用重新赋值，不用考虑“新的开始”
        if (f || i == 0)
            printf("%d", num_c[i]); 
        // 如果结果本身就是0，需要输出一个0，所以再加一个i==0的条件
    }
    
    printf("\n");
    
    return 0;
}

全排列数的生成

这道题可以用递归或非递归实现，具体方法我们在上机的时候已经统一讲过了，这里不作赘述，直接上码！

法一：递归与回溯法

#include <stdio.h>

void tape(int l, int r, int *str1, int *str2)
{
    int i;
    for(i = l; i <= r; i++)
        str1[i] = str2[i];
} // 注意回溯时，一定不是简单的交换两个位置的数字，而是把这两个位置中的整段数组都进行回溯

void swap(int *a, int *b) 
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
} // 自定义交换函数怎么写，还记得吗？

void comb(int *str, int l, int r)
{
    int i;
    int a[10];
    if (l == r) {
        for (i = 0; i <= r; i++)
            printf("%d ", str[i]);
        printf("\n");
        return;
    }
    else{
        for (i = l; i <= r; i++) {
            swap(&(str[l]), &(str[i]));
            tape(l, r, a, str);
            comb(str, l+1, r);
            tape(l, r, str, a);
        }
        return;
    }
}

int main()
{
    int i, x, a[10] = {0};
    
    scanf("%d", &x);
    
    for (i = 0; i < x; i++)
        a[i] = i + 1;
    
    comb(a, 0, x-1);
    
    return 0;
}

法二：非递归法，从右往左找到第一对递增数，以该对数的第一个数为交换对象，再从右往左找第一个比该对象大的数，相交换，再把该位置后的数组反序。

#include <stdio.h>

int a[11] = {0,1,2,3,4,5,6,7,8,9,10};

void str_rev(int s[], int hi, int low)
{
    int temp;
    for ( ; hi > low; low++, hi--) {
    temp = s[low];
    s[low] = s[hi];
    s[hi] = temp;
    }
} //该自定义函数可实现把数组反序，可以直接作为模版使用

int main() 
{
    int i, j, n, temp, flag = 1;
    
    scanf("%d", &n);
    for (i = 1; i < n; i++)
        printf("%d ", a[i]);
    printf("%d\n", a[i]);
    
    while (flag) {
        flag = 0;
        
        for (i = n - 1; i >= 1; i--) {
            if (a[i] < a[i + 1]) {
                flag = 1;
                break;
            }
        } // 从右往左找一对递增的数
        
        if (flag == 0)
            break; // 如果没找到，说明所有全排列的结果已经输出完毕
        
        for (j = n; j > i; j--) {
            if (a[j] > a[i]) {
                temp = a[i];
                a[i] = a[j];
                a[j] = temp;
                break;
            }
        }
        
        str_rev(a, n, i + 1);
        
        for (i = 1; i < n; i++)
            printf("%d ", a[i]);
        printf("%d\n", a[i]);
    }
    
    return 0;
}

字符串替换（新）

这道题的注意事项有：

1、关于文件的输入输出，文件名写对，fgets()函数的参数顺序写对；

2、不可以把输入文件里的所有字母都变成小写后再判断，因为不符合替换条件的字母需要原样输出；

3、如果要使用strcat()和strcpy()等函数完成此题，一定要判断好起始位置。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>

int main()
{
    char a[502] = {0}, b[512] = {0}, str[512] = {0}
    char c;
    int i = 0, j = 0, flag, len;
    
    FILE *in = fopen("filein.txt", "r");
    FILE *out = fopen("fileout.txt", "w");
    
    scanf("%s", a);
    scanf("%s", b);
    
    while ((c = fgetc(in)) != EOF)
        str[i++] = c;// 将文件中所有字符统一存进数组
    str[i] = '\0';
    len = (int)strlen(str);
    
    for (i = 0; i < len; i++) {
        flag = 1; // “新的开始”，每次都让flag置为1
        
        if (tolower(str[i]) != tolower(a[0])) 
            // 判断大小写是否契合，直接借用此函数即可，若参数为大写字母，则其返回值为小写字母
            fputc(str[i], out);
        else {
            for (j = 0; a[j] != '\0'; j++) {
                if (tolower(str[i+j]) != tolower(a[j])) {
                    flag = 0;
                    break;
                } // 一旦出现不匹配的位置，立即让flag为0并退出上一层循环（即for循环）
            }
            if (flag) {
                fputs(b, out);
                i = i + (int)strlen(a) - 1; // 减1是为了抵消下一次进循环的i++
            } // 如果与in数组匹配，则直接把out数组输出到文件里
            else
                fputc(str[i], out);
        }
    }
    
    fclose(in);
    fclose(out);
    
    return 0;
}

加密文件

此题注意事项包括但不限于：

1、很多同学在判断字符是否出现过时，喜欢使用循环遍历的方法，这样做固然没问题，但在数据规模较大时比较耗费时间，特别是在大作业的时候，大家感触会更深。所以可以使用used数组（类似于哈希表思想）进行判断，在大作业的时候大家也可以感受到不同算法所带来的效率差别；

2、使用数组下标的时候要统一，不要一会儿是 97-122，一会儿是 0-25，一会儿是 ‘A’-‘Z’，这样会显得很混乱，容易出错；

3、大家有时喜欢卡着真实的元素个数去定义数组的大小，其实完全没必要，建议开大一些（至少开大个一倍左右吧），这样能有效避免数组越界。

#include <stdio.h>
#include <ctype.h>

int main()
{
    char buf[512] = {0}, key[50] = {0}, str[50] = {0};
    int i, pst = 0, ch, used[50] = {0};
    FILE *in, *out;
    
    in = fopen("encrypt.txt", "r");
    out = fopen("output.txt", "w");
    
    scanf("%s", str);
    
    for (i = 0; str[i] != '\0'; i++) {
        if(!used[str[i] - 'a']) { // 如果出现过，则不写入key数组中
            key[pst++] = str[i];
            used[str[i] - 'a'] = 1; // 如果该字母以出现过，则对应used数组位置赋为1
        }
    }
    
    for (i = 'z'; i >= 'a'; i--) {
        if(!used[i - 'a'])
            key[pst++] = i;
    } // 倒序加入未出现过的字母形成最终密钥
    
    while ((ch = fgetc(in)) != EOF) {
        if(isalpha(ch))
            ch = key[ch - 'a'];
        fputc(ch, out);
    }
    
    fclose(in);
    fclose(out);
    
    return 0;
}

小型图书管理系统

本题一种简单暴力的做法是，每进行一次操作，都将所有图书重新排序。另有以下注意事项：

1、在维护图书信息时，利用变量cnt保存图书总数，并且只针对下标小于cnt的元素进行操作；

2、一些同学使用记事本查看输出结果时，发现输出的信息不能对齐，这是由于记事本中默认字体中的字符宽度是不相等的，可以切换记事本字体，例如Consolas；

3、有些同学在执行清除操作时，喜欢直接memset，但全是'\0'的字符串也会进入qsort排序中，且'\0'的字典序是最小的，因此永远会被排在前面，如果在输出时不加以判断，则会在文件最开始输出很多空内容。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

struct books {
    char name[51];
    char author[21];
    char press[31];
    char date[11];
}book[501];

int cmp(const void *p, const void *q) 
{
    return strcmp(((struct books*)p)->name, ((struct books*)q)->name);
}

int main()
{
    int cnt = 0, i  =0, op;
    char temp[100] = {0};
    
    FILE *in = fopen("books.txt", "r");
    FILE *out = fopen("ordered.txt", "w");
    
    while (fscanf(in, "%s %s %s %s", book[cnt].name, book[cnt].author, 
                 book[cnt].press, book[cnt].date) != EOF) {
            cnt++;
    }
    
    qsort(book, cnt, sizeof(struct books), cmp); // 输入完就立即进行排序
    
    while (scanf("%d", &op) != EOF) {
        if (op == 0)
            break;
        else if (op == 1) {
                scanf("%s %s %s %s", book[cnt].name, book[cnt].author, 
                      book[cnt].press, book[cnt].date);
                cnt++;
                qsort(book, cnt, sizeof(struct books), cmp);
            // 插入后进行排序，如果没有此步骤，则后续查找时，可能导致输出的图书顺序有误
        }
        else if (op == 2) {
            scanf("%s", temp);
            for (i = 0; i < cnt; i++) {
                if (strstr(book[i].name, temp) != NULL) // 使用strstr函数直接进行查找
                    printf("%-50s%-20s%-30s%-10s\n", book[i].name, 
                           book[i].author, book[i].press, book[i].date);
            }
        }
        else if (op == 3) {
            scanf("%s", temp);
            for (i = 0; i < cnt; i++) {
                if (strstr(book[i].name, temp) != NULL) {
                    for(int j = i; j < cnt - 1; j++)
                        book[j] = book[j + 1]; // 将后续图书全部前移，即可实现删除功能
                    i--; // 因为前移，需抵消下次进循环的i++影响
                    cnt--;
                }
            }
        }
    }
    
    qsort(book, cnt, sizeof(struct books), cmp); // 最后再排一次序，以防万一
    
    for(i = 0; i < cnt; i++) {
        fprintf(out, "%-50s%-20s%-30s%-10s\n", book[i].name, 
                book[i].author, book[i].press, book[i].date); // 对齐方式应该如此写
    }
    
    fclose(in);
    fclose(out);
    
    return 0;
}

面向对象的数据结构 —— 数组篇

引入

同学们在解决实际问题时，往往会在问题理解和编程实现两方面遇到困难。我们以第三次作业第二题“空闲空间分配”为例。
题意理解的问题形如
查找目标的规则是什么，我要如何判断
如果没找到，我要怎么标记
如果空间一点不剩，我需不需要特判
编程实现的问题形如
新的节点如何申请
删除节点怎么写，哪些指针要修改
什么是循环链表，怎么遍历
事实上，这两大问题对应我们程序中的两大部分
主函数main的结构，如各种循环和分支的嵌套，这是我们解决问题的逻辑
每个循环或分支内的具体语句，如一次赋值、一次拷贝、一次遍历等
这两大部分，也就对应两类常见 bug
漏了一种if的情况，忘记把flag重新置为 0 等逻辑问题
访问了空指针，下标数错，忘加 ‘\0’ 等基本操作问题
事实上，如果把所有代码都写在main里，我们很难分清也很难定位具体的 bug。一种做法是封装一些函数，这种做法简化了代码，增强了代码的可复用性，但不妙之处在于，我们每做一道题，就要把这些内容重新写一遍，因为每道题用到的数据类型是不同的 —— 这道题的struct里的数据项只有一个int，而下一道题变成了一个double和一个char[20]，我们就需要把所有的函数都修改一遍。
所以，单纯地封装insert_node delete_node等函数，仍然不是最理想的做法。

对象（Object）

今天我们仅讨论线性表中的数组，为了便于说明，我们仅以int型的数组为例。事实上，只要稍加改进，我们就可以写出适配任何数据类型（包括结构体）的数组。

可是，数组有什么好写的呢？我们写下int arr[10] = {0};，不就定义了一个数组吗？我们可以通过下标访问、也可以通过指针访问，我们可以读取内容、也可以赋值。然而，正是因为我们频繁地在代码中写下printf("%d\n", arr[index]);等直接操作数组的代码，我们才会犯下下标越界等导致程序崩溃的错误。如果我们在程序中加入很多条件判断，保证每一次操作的合法性，又会徒增代码量，和我们程序的运行逻辑相混淆。

事实上，直接定义的数组只是一个存放数据的“变量”。如果将存放数据的数据结构，其相关属性，以及在数据结构上的操作封装，我们就得到了一个对象。以今天介绍的数组为例，一个“数组对象”应当包括如下三个方面

存储数据的数据结构，即数组本身（为了实现可变长数组，我们用一个指针管理数组并用malloc分配空间，而非直接写一个定长数组）
属性，如当前数组的最大容量、当前数组的元素个数
一系列函数，提供初始化、插入、销毁的功能

为了实现上述目标，我们首先定义自己的数组类型

#define INIT_SIZE 10
	// 这里定义了一个宏，设置数组的初始容量。
	// 后续初始化数组时，如果没有指定容量，则先开辟 10 个 int 的大小
typedef struct array {
    int *head;		// 数组首地址
    size_t size;	// 数组的最大容量
    size_t cur;		// current，当前数组的元素个数
} array_t;			
    // ‘_t’结尾是 C 的经典代码风格，表示这是 typedef 的一种新类型，即我们的“数组类型”

// 以后当我们写下
array_t arr1, arr2;
// 等代码时，就可以说，我们现在拥有了两个数组对象，分别叫 arr1 和 arr2

现在，我们有了自己的数组类型，也可以定义自己的数组对象。当然，arr1[1]等原有的操作将不被允许了，所有的操作都将通过函数进行。在每一个函数中，我们只需要将数组对象 —— 实际上是这个对象的地址 —— 传入函数，就可以对某一个具体的数组对象进行操作。

初始化与销毁

int main()
{
    array_t arr;            // 定义了一个数组对象
    array_init(&arr, 100);  // 初始化数组对象，开辟 100 个 int 的容量
    array_destroy(&arr);    // 销毁数组对象
    return 0;
}

为了实现这样简洁的代码，我们需要自己设计一系列函数

int array_init(array_t *arr, size_t size)
{
    /* 初始化数组
    	参数
       		`arr`  array_t 的指针，即 struct array 的指针，代表数组对象
       		`size` 数组的起始容量，如果小于等于 0，则默认开辟 INIT_SIZE 个
       	返回值
       		如果初始化成功返回 0，否则返回 -1
    */   
    
    if (arr == NULL) return -1;  // 如果没有传入数组对象，则失败
    int real_size = (size > 0) ? size : INIT_SIZE; 
                                 // 如果参数 size 非正，则使用预先定义的 size
    if ((arr->head = (int*)malloc(sizeof(int) * real_size)) == NULL) {
        return -1;  // 如果 malloc 失败，则函数直接返回
    } else {
        arr->size = real_size; // 更新数组的最大容量
        arr->cur = 0;          // 设置当前元素个数为 0
    }
    return 0;  // 成功则返回 0
}

void array_destroy(array_t *arr)
{
    /* 销毁数组
       参数
       		`arr`  array_t 的指针，代表要销毁的数组
    */
    
    if (arr == NULL) return;
    free(arr->head);  // 释放数组的数据区
    arr->head = NULL; // 将数组头指针改为空值
    arr->size = 0;    // 将数组最大容量改为 0
    arr->cur = -1;    // 将数组元素个数改为无效值 -1
    return;
}

数组的生长

传统的数组大小是固定的，如果访问越界（有可能是下标过大，也有可能是下标为负数）将产生得到随机值、程序崩溃等问题。这里，我们的数组并非直接定义，而是通过malloc动态申请，这就为其生长提供了可能。我们规定，每当数组生长的时候，容量增加原来的一倍。当然，我们不应在程序中直接调用此函数，而是让“插入元素”等函数自动调用。

int array_grow(array_t *arr)
{
    /* 将数组容量扩大一倍
       参数
       		`arr`  array_t 的指针，代表要扩大的数组
       返回值
       		成功返回 0，失败返回 -1
    */
    
    if (arr == NULL) return -1;
    int old_size = arr->size;     // 生长前的容量
    int new_size = old_size * 2;  // 生长后的容量
    int *p = NULL;                // 管理新分配的空间的指针
    if ((p = (int*)malloc(sizeof(int) * new_size)) == NULL) {
        return -1; // 申请更大的空间，如果失败则直接返回
                   // 当然哪怕这种情况发生，原有数组中的内容仍然保存
    } else {
        for (int i = 0; i < old_size; i++) { // 循环复制原数组内容
            p[i] = arr->head[i];
        }
        free(arr->head);       // 释放原数组的数据区
        arr->head = p;         // 更新数组首地址
        arr->size = new_size;  // 更新数组最大容量
    }
    return 0;
}

元素的插入

数组的插入可以分成两类 —— 尾部插入和中间插入。前者只需要传入新的元素，后者还需要获取插入的下标。这里我们仅实现前者。插入新元素，则有可能会出现越界的情况，所以这个函数需要自行判断会不会越界，如果会，则需要主动调用数组生长函数扩大空间。我们通过一张图更直观地了解数组的容量size和元素数量cur的关系。

int array_push(array_t *arr, int val)
{
    /* 在数组 `arr` 尾部插入元素 `val` 
       成功返回 0，出错返回 -1
    */
    
    if (arr == NULL) return -1;
    if (arr->cur == arr->size) {      // 这种情况表示数组已满，需要 grow
        if (array_grow(arr) == -1) {
            return -1;  // 如果 grow 失败则直接返回
        }
    }
    arr->head[arr->cur] = val; // 在尾部插入元素
    arr->cur++;                // 更新元素个数
    return 0;
}

上述若干函数为我们实现了一些针对数组对象的基本操作，当然这还远远不够。你可能需要自己书写其他函数，例如

int array_isempty(array_t *arr);
    // 判断数组 `arr` 是否为空。空返回 1，非空返回 0，出错返回 -1

int array_get(array_t *arr, int index);
    // 获取数组 `arr` 中下标为 `index` 的元素值并返回

int array_index_of(array_t *arr, int val);
    // 获取数组 `arr` 中值为 `val` 的元素下标并返回，如果未查找到返回 -1

int array_insert(array_t *arr, int index, int val);
    // 在数组 `arr` 下标为 `index` 的位置插入元素 `val`。成功返回 0，出错返回 -1

int array_set(array_t *arr, int index, int val);
    // 将数组 `arr` 中下标为 `index` 的元素设置成 `val`。成功返回 0，出错返回 -1

int array_remove_index(array_t *arr, int index);
    // 将数组 `arr` 中下标为 `index` 的元素删除。成功返回 0，出错返回 -1

int array_remove_val(array_t *arr, int val);
    // 将数组 `arr` 中值为 `val` 的元素删除。成功返回 0，出错返回 -1

size_t array_size(array_t *arr);
    // 获取数组 `arr` 的元素个数并返回，出错返回 -1

size_t array_sizeof(array_t *arr);
    // 获取数组 `arr` 中数据部分的总字节数，功能类似传统的 sizeof(数组名)。出错返回 -1

int *array_to_array(array_t *arr, int *ret);
    // 将数组对象 `arr` 转换成基本数组，存于 `ret` 中并返回。出错返回 NULL

int *array_subarray(array_t *arr, int from, int to, int *ret);
    // 将数组对象 `arr` 中下标为 [from, to) 的子序列转换成基本数组，
    // 存于 `ret` 中并返回。出错返回 NULL

int array_sort(array_t *arr, int mode);
    // 将数组 `arr` 排序，规则由 `mode` 指定(如 0 为升序，1 为降序)。成功返回 0，出错返回 -1

这些函数看起来较为麻烦，但是一经实现，你就有了独属于自己的一套模板。未来，你可以将它们扩充为适配任何类型的数组，甚至把它们做成一个头文件，每次使用时，只需要#include <myarray.h>，多是一件美事啊。实现了这些函数之后，你的代码里将不再出现大量的中括号、赋值和下标，取而代之的是 set、get、remove 等函数的调用，每一次完成一个操作，呈现在代码中的都不再是晦涩的运算符，而是具有自然语言含义的函数名，那你的代码的可读性也就增加了。

如果同学们实现了这 12 个函数中的 8 个及以上，可以来找助教兑换小奖品。

另外，这次封装的数组对象，也启发我们思考两个问题

如何封装一个链表
如何实现从int到任意数据类型的扩充

我们会在后续猪脚说中迭代地更新这部分内容。

为什么数组比链表快

已经了解过第三次作业第五题“词频统计”的同学，可以尝试用数组和链表分别实现一下。假设我们用数组实现时不用二分查找，而仍使用较低效的顺序查找，我们仍可从 judge 平台上反馈的运行时间看出，数组比链表快。这是为什么呢？
理论上，数组的查找时间复杂度为 $O(n)$，插入的时间复杂度也为 $O(n)$；链表的查找的时间复杂度为 $O(n)$，插入的时间复杂度为 $O(1)$。为什么数组在实践中更加高效呢？这还要从一个故事说起……

小z决战高考的故事

高中生小z打算奋战百天，决胜高考，誓死考上 BUAA。这天我们来到他的教室，看到如下场景

如图，小z的课桌上摆放了一个书立，他的课桌有一个抽屉，他的座位旁边放了一个书箱，在教室的后面还有一个储物柜。我们不难想象他会在这些地方各自存放什么东西，比如

书立里放着刚考完的月考卷和今晚要做的作业；
抽屉里放着各科的复习书和辅导材料；
书箱里存放各科的课本，以备必要时参考；
储物柜里放着几个月前做过的卷子~~和《故事会》~~。

按照上面的顺序，我们发现以下规律：储物量 —— 从小到大、存取物品的速度 —— 从快到慢（比如书立中的材料只需要直接抽出来、插回去，而储物柜中材料的存取还需要起身走动）、存放的内容 —— 从重要到不重要、访问频率递减。

很显然，这种安排符合逻辑：很快就会用到的东西就就放在手边，相对无关紧要的东西存放在别的地方。这给了我们什么启示呢？

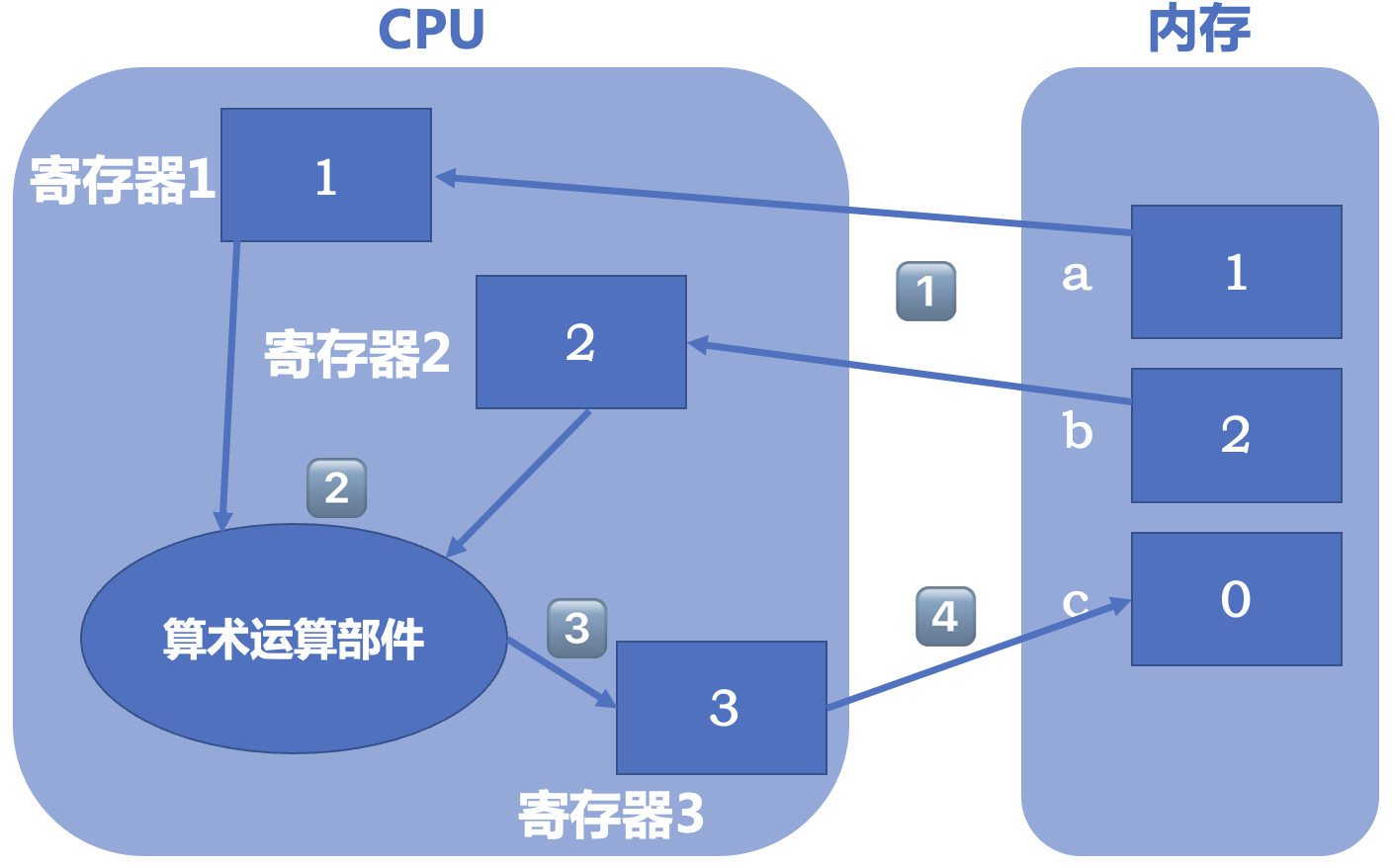
计算机的存储层次

计算机的存储系统从高到低大致可以分为四层：寄存器，高速缓存，内存和外存。

外存就是硬盘等设备，如同学们常听到的“512G 的硬盘”“256G 的 iPhone”等，这些指的就是硬盘容量，U 盘等设备属于可移动的硬盘。
文件（包括程序）一般都存放在外存中，当它们要开始运行时，就要先加载到内存；另外，我们已经知道，程序中定义的变量、数组等也都存放在内存中。
寄存器位于 CPU（中央处理器）中，存放在内存中的数据要进行运算，必须先放进寄存器。例如，我们写int a = 1, b = 2; int c = 0; c = a + b;，则内存中会先有a b c三个变量，进行第三步的运算时，先把a和b放进两个寄存器中，在 CPU 完成计算后，结果 3 被放进另一个寄存器，最后将其中的内容存放回内存中c的位置。

当然，不同层级的存储设备其容量、速度和成本都是不同的。寄存器速度最快，但是容量很小（只能存放一个数）且成本高昂；内存容量比较大，但是读取和写入的速度都很慢。为了缓解 CPU 的高速和内存的低速的矛盾，人们发明了高速缓存技术。

局部性原理
局部性原理可以分为时间局部性原理和空间局部性原理。
1
for (int i = 0; i < n; i++) arr[i] = i;
时间局部性原理：刚访问过的存储单元，不久后很可能会再次访问。例如上例中的循环变量i，在每一次循环中都会被访问若干次。
空间局部性原理：刚访问过的存储单元附近的单元，不久后更可能被访问。例如上例中，我们访问了arr[0]，不久后就会访问其附近的arr[1] arr[2]等存储单元。

高速缓存是一类存储设备，它们的存取速度远高于内存，但是容量比较小。根据局部性原理，把内存切割成很多块，把最近用到的一些块放进高速缓存中，每次需要访问内存时，优先到高速缓存中查找，如果找到，就可以不用访问内存，而是直接对高速缓存中的数据进行操作。如此一来，我们就可以减少直接访问内存的次数，从而提高了程序运行的效率。

正如同小z的例子，他会把更常用到的材料放在离手边更近的地方，从而提高寻找的效率。当然，手边的空间是有限的，他不能保证所有用到的材料都在手边；当他在手边没有找到想要的材料时，他还是得费点力气去储物柜里寻找。

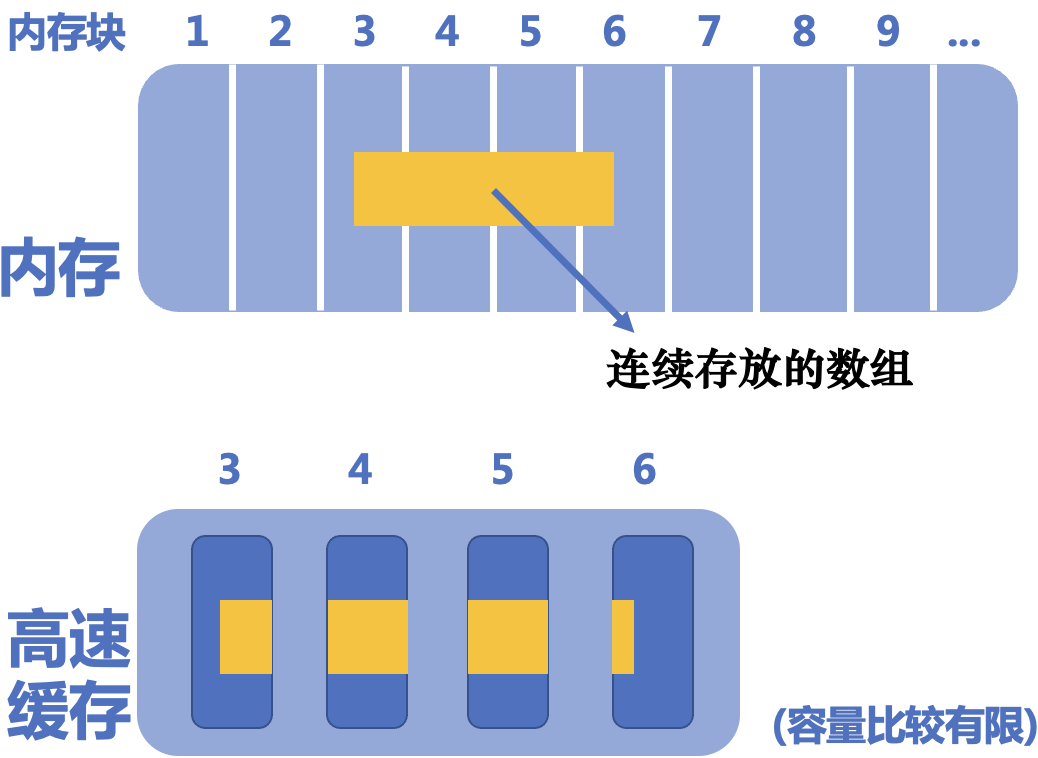
问题解决

正如前文所述，内存中的一些块会被拷贝进高速缓存中，以加快访问数据的速度。

数组在内存中是连续存放的，因此，它们更有可能被连续地放进高速缓存中，从而在访问数据时，能够直接在高速缓存中找到，避免了查找低速的内存。

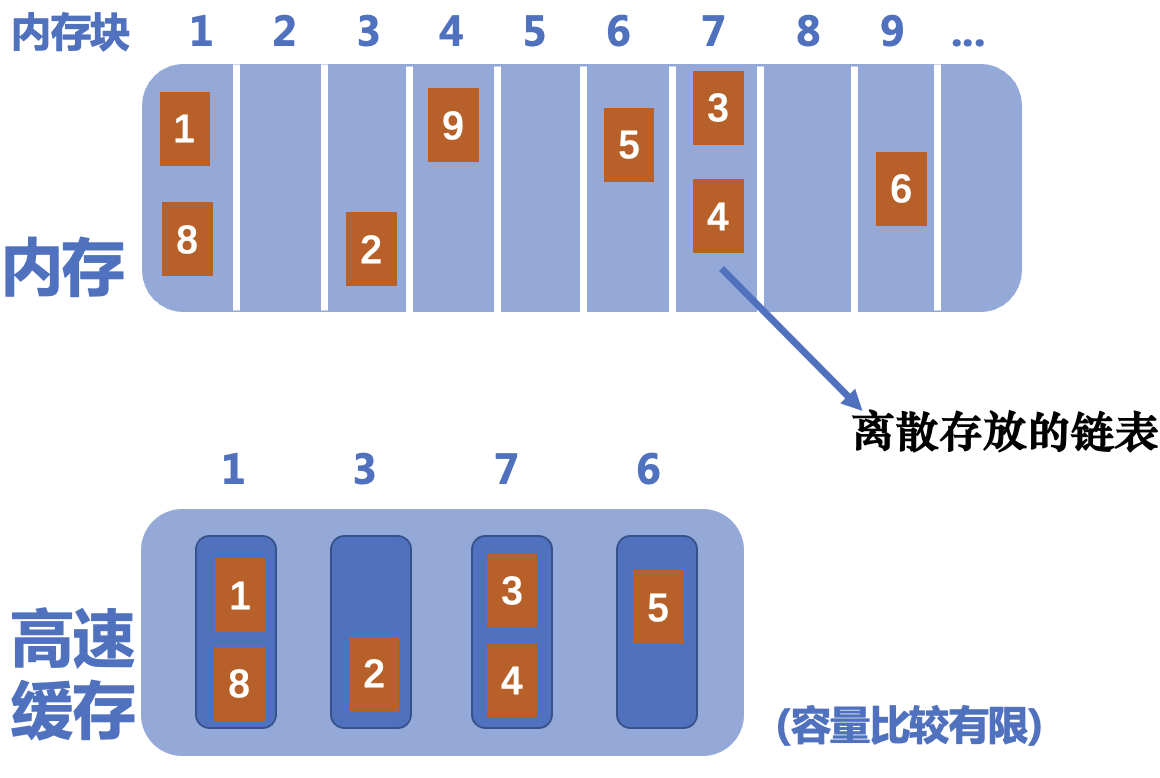
链表的每一个节点都是malloc来的，这类动态申请的空间，离散地分布在内存中。在遍历链表的过程中，哪s怕某个节点在高速缓存中，也不能保证后续节点在高速缓存中，因此访问内存的次数大大增加，程序运行的时间增加。

了解计算机存储相关原理并非多余或超纲。一方面，几乎所有信息类专业都要求掌握计算机组成原理 / 计算机硬件基础 / 计算机体系结构等科目；另一方面，多年来数据结构的大作业都是基于词频统计的，并且会根据程序运行时间进行排名，提前了解连续存储和链式存储的特点，对同学们选择解题方法有很大帮助。

Author: diandian, Riccardo

Diandian Honey Pot