猪脚说第六期

容易忽视的 bug

判断空指针与访问空指针

在给大家 debug 的时候，我们发现了一个普遍存在、且大多数同学喜欢写但是其实是错误的写法，并且这个写法往往导致了程序报SIGSEGV或运行时间过长的错误，请看如下代码：

struct node {
  int x;
  struct node *next
};
	
// in main:
struct node *p = list;
while (p->x != 0 && p != NULL) {
  // do something
  p = p->next;
}

那么这段代码是如何访问到空指针的呢？这其中的关键就在while的判断里。

如果在某次循环后，p已经是空指针，逻辑上来说，while条件逻辑值为假，不会再进入循环。但程序执行时，两个条件都要进行判断，所以当p为空指针时，依然需要首先执行p->x != 0的判断，才能进一步判断是否进入循环，由此，程序便访问到了空指针。

改进方法很简单，只需要在while条件里只保留p != NULL，而把其余所有判断移到while循环内部进行：

while (p != NULL) {
  if (p->x != 0) {
    // do something
    p = p->next;
  }
  else
    break;
}

因此，上述例子告诉我们，在进行链表循环遍历时，不能将空指针判断与其他需要访问结构体成员的相关判断放到一起，在循环判断里只保留空指针判断，而其他涉及结构体成员的判断放到循环内部一开始执行。这也是我们一直强调的事情：请把你代码的业务逻辑和在数据结构上的基础操作分离。

循环链表的遍历输出

很多同学使用如下方法进行一个循环链表的遍历输出：

for (p = list; p->next != list; p = p->next)
  printf(/* args */);

该代码错误原因很明显，即当p为list的前一个节点时，就不会再进入for循环了，因此少打印了一个节点。修改方式当然可以是，在跳出for循环后，再对当前的p节点进行一次打印，但未免稍显繁杂，因此可以采取如下方式：

p = list;
do {
  if (p == NULL)
    break;
  printf(/* args */);
  p = p->next;
} while (p != list);

## 链表的规范化操作

> 这部分主要针对课件中链表的基本操作，请掌握不牢的同学再次自查，**千万不要出现基本操作出错的情况！** 此外我们给大家提几点使用链表的建议。
>
> - **少用`typedef`。**很多同学代码中出现大量的标识符，如`node` `_node` `Node` `PNode` `Nodeptr`等，这很可能导致某个地方将复合数据类型和它的指针类型相混淆，造成不必要的麻烦；另一方面，作为并不是很系统的一个程序，这么自定义类型别名会给看你代码的人带来困扰。
> - **规范命名**。数据域中的变量名应当与实际情况相符合，如`char book_name[64];` `long stu_id;` `int wait_time;`等，切忌`a` `b` `c` `x` `y` `z`（除非这个结构体就是表示某种特定的数学符号，如坐标`(x, y)`或图的边`<u,v>`）；**指针域应当统一写`next`和`prev`**。
> - **不要用全局变量，尤其是`head`头指针。**

### 统一口径

<img src="/images/assets6/截屏2023-03-29 08.53.08.png" alt="截屏2023-03-29 08.53.08" style="zoom:50%;" />

我们以上图所示的**单向链表**为例。假设我们的链表的节点声明如下**（什么是声明、什么是定义？）**

```c
struct node {
    int val;           // 这是个没有意义的名字！实际使用时最好不要这么写，这里只是举个小例子
    struct node *next;
};

遵循不用全局变量的原则，我们把一切变量都定义在main中

int main()
{
    struct node *head;
    // call functions
    return 0;
}

当然，作为局部变量的head，如果直接传入各个函数，并不能修改其值，正如同在main中调用void f(int i) { i = 100; }并不能修改main中int变量的值。所以，我们统一传入**struct node的二级指针作为参数，函数调用时统一写&head**。这里假定函数都没有返回值。

链表的初始化

链表的初始化需要做的事情是将head指针设置成NULL。

void initlist(struct node **phead)
{
    // 功能：初始化链表
    *phead = NULL;
}

链表的插入

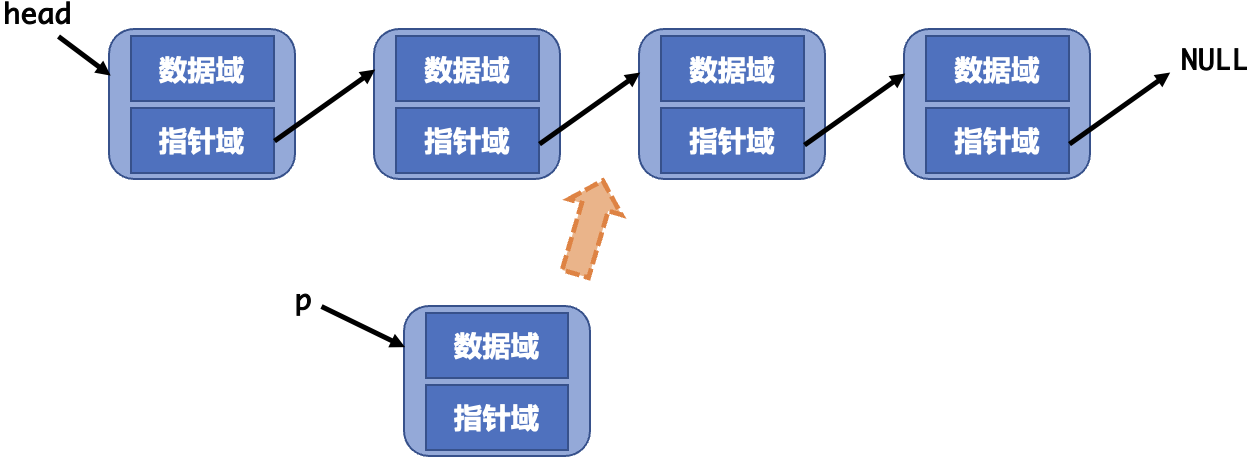
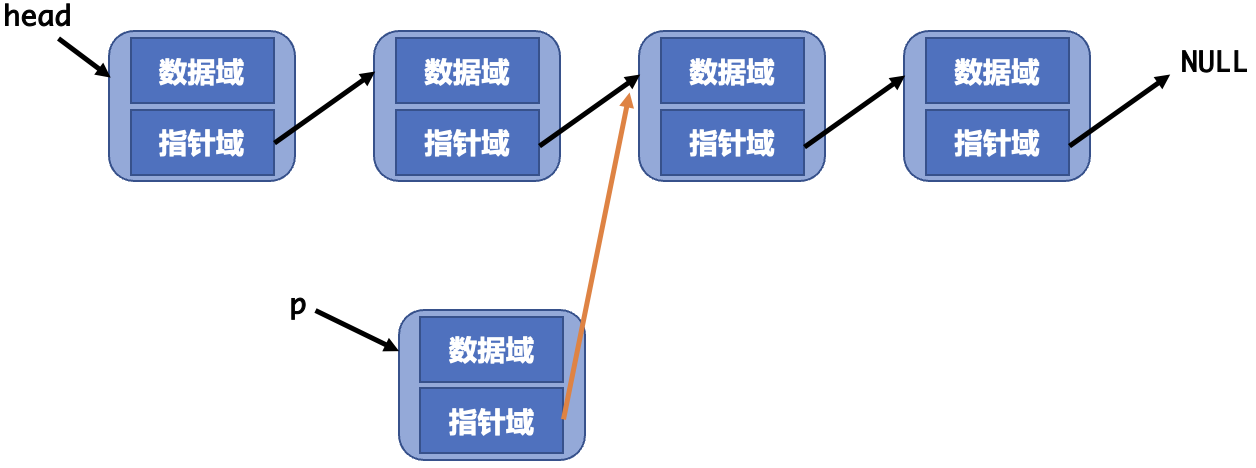
链表的插入需要做三件事

• 通过malloc申请一个新节点并设置数据。
• 假设我们要在节点p的后面插入，则需要将新节点的指针指向p的后一个节点。
• 将p的指针指向新节点。

void insertlist(struct node **phead, struct node *p, int val)
{
    // 在节点 p 后插入新节点，其数据为 val
    
    struct node *head = *phead;
    // ------ 创建新节点 ------
    struct node *q = (struct node*)malloc(sizeof(struct node));
    	/* 这里其实应该加入错误判断的代码，如果 malloc 失败，则 q 为 NULL
    	   当然我们写的小程序一般不会有问题，除非你开了【某些杀毒软件】
    	   if (q == NULL) {
    	       perror("malloc error");
    	         // 这个函数声明在 <stdio.h> 中
    	         // 能够在标准错误(屏幕)上输出 malloc error: xxx
    	         // xxx 为此函数解析的错误信息
    	         // 当然你也可以写 `fprintf(stderr, "malloc error\n");`
    	         // 或 `printf("malloc error\n");`
    	       exit(1); // 或 `return;`，前者直接结束程序，后者只是返回 main
    	   }
    	*/
    q->val = val;
    q->next = NULL;
    // -----------------------
    if (head == NULL) {       // 如果链表为空
        head = q;             // 头节点就是新节点
    } else if (p == NULL) {   // 如果在头节点之前插入
        q->next = head;       // 新节点的下一个节点就是原来的头节点
        head = q;             // 头节点改为新节点
    } else {
        q->next = p->next;
        p->next = q;
    }
    *phead = head;            // 更新 main 中的 head 变量
}

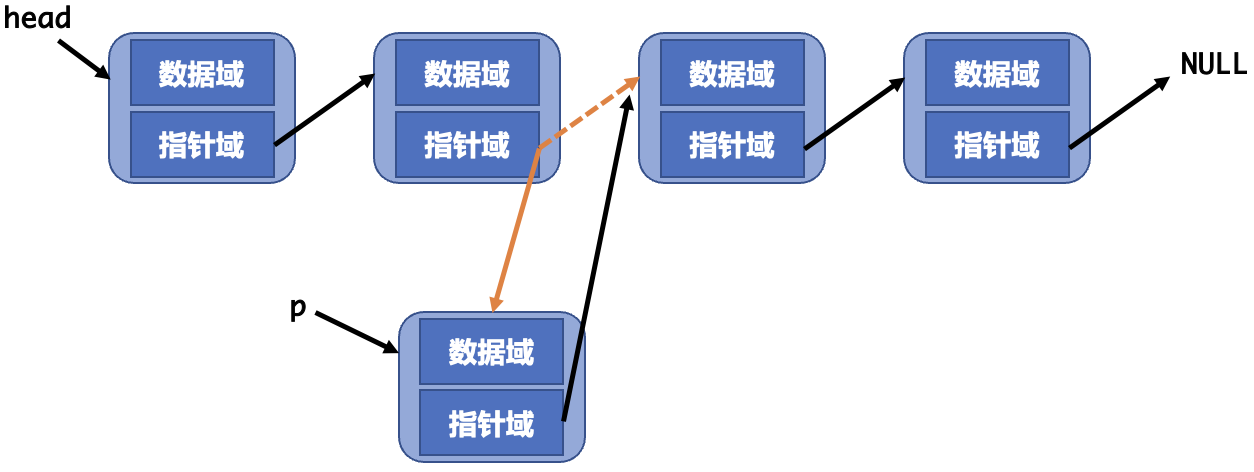
我们对三种不同的插入进行讨论。参数中的p表示我们要在哪个节点后插入，其中，当head为NULL时，链表必然为空，则直接给头节点赋值即可；如果链表非空，而插入的位置p为空，则说明要在头节点之前插入 —— 因为这里的参数p，必然是通过调用某个查找函数得到的，那个查找函数遍历链表，应当有如下的功能

• 找到链表中符合条件的节点，则返回该节点的指针。
• 未找到符合条件的节点
  • 如果这是无序链表，就返回尾节点的指针，便于在尾后插入。
  • 如果这是有序链表（假设从小到大），如果我们要找的比表中任何一个数都要小，则返回NULL，表示未来应该插在链表的头；如果我们要找的比表中任何一个数都要大，则返回尾节点的指针，表示未来应该插在尾后。

上述说明或许稍显复杂，我们可以这么想：p标识我们要插入的位置，在链表的中间插入或在尾后插入，操作是相同的，所以p只要是一个节点的指针即可；只有在头节点前插入是特殊的，此时p应该为特殊值NULL。

链表的删除

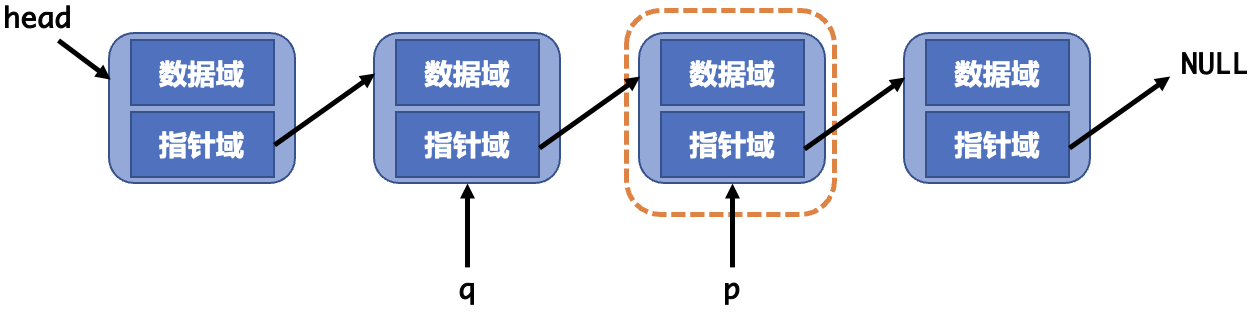
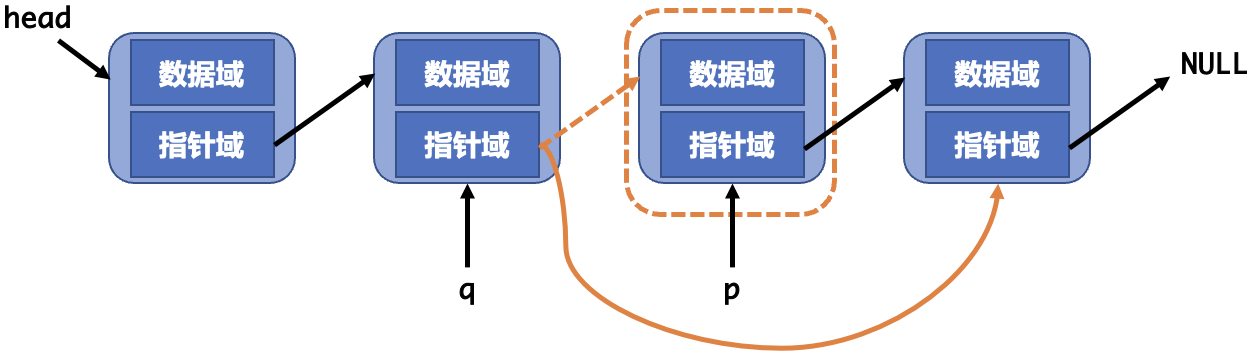
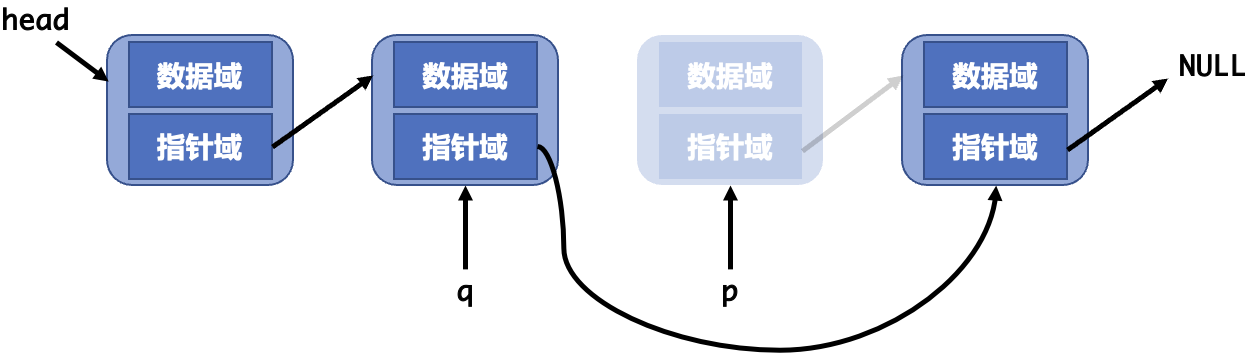
链表的删除需要做三件事

• 找到需要删除的节点及其前序节点。
• 将前序节点的指针指向需要删除节点的下一个节点。
• 释放要删除的节点。

void deletelist(struct node **phead, struct node *p)
{
    // 删除节点 p
    struct node *head = *phead;
    struct node *q = head, *r = NULL;    // q 从头开始遍历，r 为 q 的前一个节点
    for ( ; q != p; r = q, q = q->next)
        ;
    // for 循环结束后，q 指向 p，r 指向 q 的前一个节点
    if (r == NULL) {        // 如果删的是头节点
        head = q->next;     // 改变头节点
        free(q);            // 释放原来的头节点
    } else {
        r->next = q->next;
        free(q);
    }
    *phead = head;          // 更新 main 中的 head
}

链表的遍历

void traverselist(struct node *head, void (*visit)(struct node *))
{
    // 遍历链表中的每一个节点，对于每一个节点，调用函数 visit 进行访问
    // 第一个参数 head 即头节点，由于遍历并不会修改 head，所以不用传二级指针
    // 第二个参数为一个函数指针，表示访问方式
    //     - 这个函数的返回值是 void 类型
    //     - 这个函数需要接收一个 struct node * 类型的参数
    // 假设我们有
    //    void visit_1(struct node *p) { printf("p->val: %d\n", p->val); }
    // 和
    //    void visit_2(struct node *p) { printf("(p->val)^2: %d\n", 
    //                                             (p->val) * (p->val)); }
    // 则可以在 main 中通过不同访问方式、打印不同信息
    //    traverselist(head, visit_1); traverselist(head, visit_2);
    
    if (head != NULL) {
        for (struct node *p = head; p != NULL; p = p->next) {
            visit(p);
        }
    }
}

链表的销毁

销毁链表即free链表的每一个节点，只写free(head);是必然不可行的，除非链表中只剩下一个头节点。另一方面，一旦当前节点被free，则无法找到下一个节点，所以，销毁链表需要从最后一个节点开始。然而，找到了最后一个节点，其前一个节点又得从头遍历才能找到，所以，这里我们通过递归实现。具体的原理请画草图分析，这里不再赘述。

void destroylist(struct node **phead)
{
    // 销毁链表，在 main 中应调用此函数
    // 其具体递归实现放在 recursive_free 中
    
    struct node *head = *phead;
    recursive_free(head);
    *phead = NULL;  // !! 将 main 中的 head 改为 NULL，防止销毁后再访问 !!
}
void recursive_free(struct node *p)
{
    // 释放 p 及其后的节点
    
    if (p->next != NULL) {        // 如果 p 后面还有节点
        recursive_free(p->next);  // 释放 p 后面的所有节点
    } 
    free(p);                      // 释放 p
}

关于free函数

我们摘要了手册中关于free函数的一些内容：

void
  free(void *ptr);

The free() function frees allocations that were created via the preceding allocation functions.[allocation: (内存)分配；preceding: 上述的]

The free() function deallocates the memory allocation pointed to by ptr. If ptr is a NULL pointer, no operation is performed. [deallocates: 释放、回收、解除分配]

这里，“前面提及的内存分配函数”指的是包括malloc在内的以calloc valloc realloc为代表的 C 库内存分配函数，有兴趣的同学可以自己 STFW（Search the Friendly/F**king Web）一下。申请来的空间需要释放，这就是free的功能，该空间通过指针ptr指出。这其中的注意事项包括

• free将ptr所指的内存空间全部清理，但并不会改变ptr还指在那里的既定事实。

  int *pi = (int*)malloc(sizeof(int));
  *pi = 10;
  printf("before free, *pi = %d\n", *pi);
  free(pi);
  printf("after free, *pi = %d\n", *pi); // 合法，不会崩溃，大概率输出不是 10 的数

• free同一片内存多次程序会崩溃。

  void *p = malloc(1);
  free(p);
  printf("first free success\n");  // 会输出
  free(p);
  printf("second free success\n"); // 不会输出

• free(NULL);是安全的，这种情况下无事发生。

• 综上三点，好习惯是：写完free(p);立即写p = NULL;。一方面可以防止你在释放空间后再次访问，因为此后访问空指针p程序会直接崩溃而非访问到一个奇怪的值；另一方面可以防止你不小心再次free而导致程序崩溃，因为free空指针是安全的。这里的区别在于，如果你无意中访问已经被free的空间，并不会报错，只是会得到错误数据而你找不出 bug，所以需要程序崩溃来提醒你错误访问了；如果你忘记考虑某些特殊情况而不慎多次free同一片内存，为了防止崩溃并简化代码，将指针设置成NULL是一个不错的选择。

链表结构的拓展

上述链表操作的基本思路和课件中相同，无非是节点的申请、链表头的维护和指针域的改变。在编程的时候，我们无需关心自引用结构中的底层逻辑，即不需要思考地址之类的问题，而是用更加上层的视角审视代码。此犹言

• head p q r next等只是标识符，它们就代表了节点，访问时统一通过->即可。
• p = p->next等操作只是“挪一下位置”，而不应该细化为地址的赋值。
• 插入删除等函数中，一切指针赋值操作，应抽象为“声明了一个指向关系”。访问一个节点，我们要让p“指向”它；将 A 连接上 B，我们要让 A 的next“指向”B。所以，使用链表时，必须画图。

next ? next !

我的next是你，你的next是他 —— 于是，我连接你，你连接他。链表的实现思路使我们第一次看到了指针的作用，仅仅在结构体中增加了next成员，我们就能够创造出一种崭新的线性表。

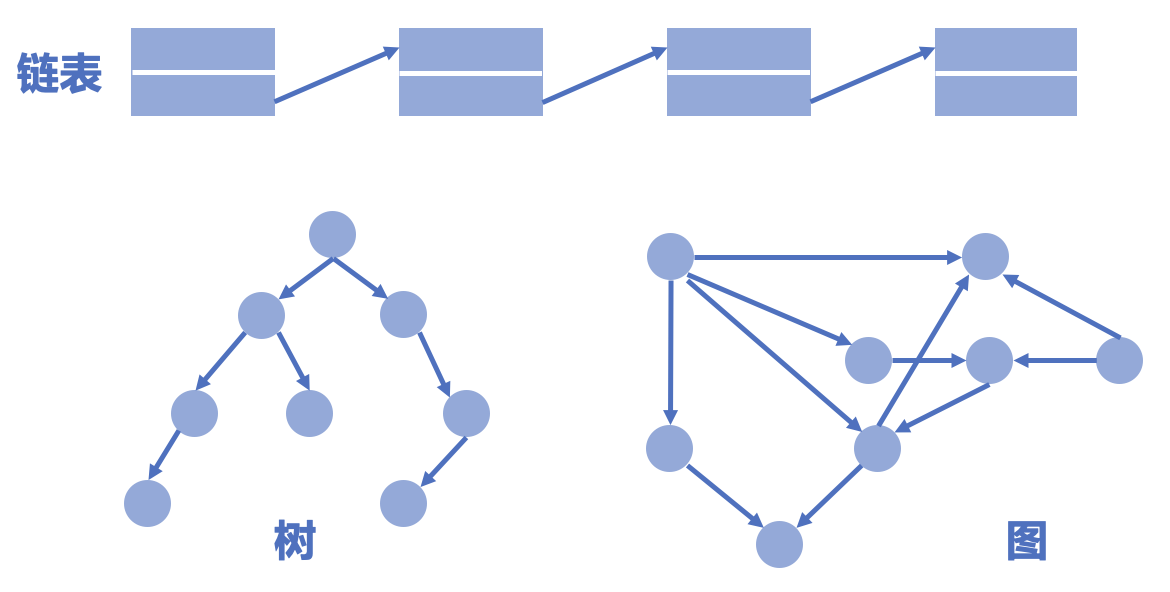
还记得这张图吗？我们已经实现了其中的链表，那么树和图应该怎么实现呢？

• struct node *left, *right;，假设struct node中有两个指针成员，那么一个struct node就可以最多指向两个其他的struct node，这就对应着二叉树结构。
• struct node *neighbors[10];，假设struct node中有一个指针数组成员（其中包含了 10 个指针），那么一个struct node就可以最多指向十个其他的struct node，这就对应着图结构。

可见，有了指针，我们就在节点上定义了“指向”关系，A 指向 B，当且仅当通过 A 可以访问到 B。在程序里，指针存放节点的地址，于是通过一个节点可以访问到其他节点，这就实现了“指向”关系。

其实，我们可以用更加抽象的语言定义这件事情。设我们有如下集合
$$
A={e_1, e_2, \cdots, e_n}
$$
符号
$$
<a,b>
$$
用来表示 $a$ 和 $b$ 有关系。注意，这里有顺序问题，即如果 $a \neq b$ ，则 $<a,b>$ 和 $<b,a>$ 是不一样的关系。在我们的语境中，**$<a,b>$ 可以表示通过 $a$ 可以访问到 $b$，也就是 $a$“指向” $b$**。

假设上述集合 $A$ 中的每个元素都是单向链表 $L$ 的节点，则 $L$ 实际上就是如下的集合
$$
L={<e_1, e_2>,<e_2,e_3>,\cdots,<e_{n-1}, e_{n}>}
$$
假设上述集合 $A$ 中的每个元素都是双向链表 $L’$ 的节点，则 $L’$ 实际上就是如下的集合
$$
L’={<e_1,e_2>,\cdots, <e_{n-1}, e_n>,<e_n,e_{n-1}, \cdots,<e_2,e_1>}
$$
所以我们发现，链表之所以为链表，就在于其节点通过指针域描述了一种“指向”关系，至于数据域中有什么内容，是无关紧要的。换言之，我们如果对指针域进行适当的扩充、封装，配合上一系列函数，就可以实现通用链表。

一种双向链表的构想

我们发现很多同学喜欢使用双向链表，其实在作业题中并没有太大必要使用，徒增一个指针成员只会增加犯错的几率。

我们使用链表时其实只会顺序地遍历链表，并不会逆序遍历，另外，[2.5 节](#2.5 链表的销毁)提到的链表销毁函数，也给了我们逆序遍历的思路。所以，使用指向前一个节点的指针，无非是为了在某些特定的插入删除操作中，快速地找到前一个节点，进而修改前一个节点的next指针。实际上，我们想要快速访问前一个节点的next指针，只需要拥有那个next成员的地址即可。换言之，这里的prev指针，可以不是前一个节点的指针，而是前一个节点的next成员的指针。

于是，我们可以构造一种新的链表结构。

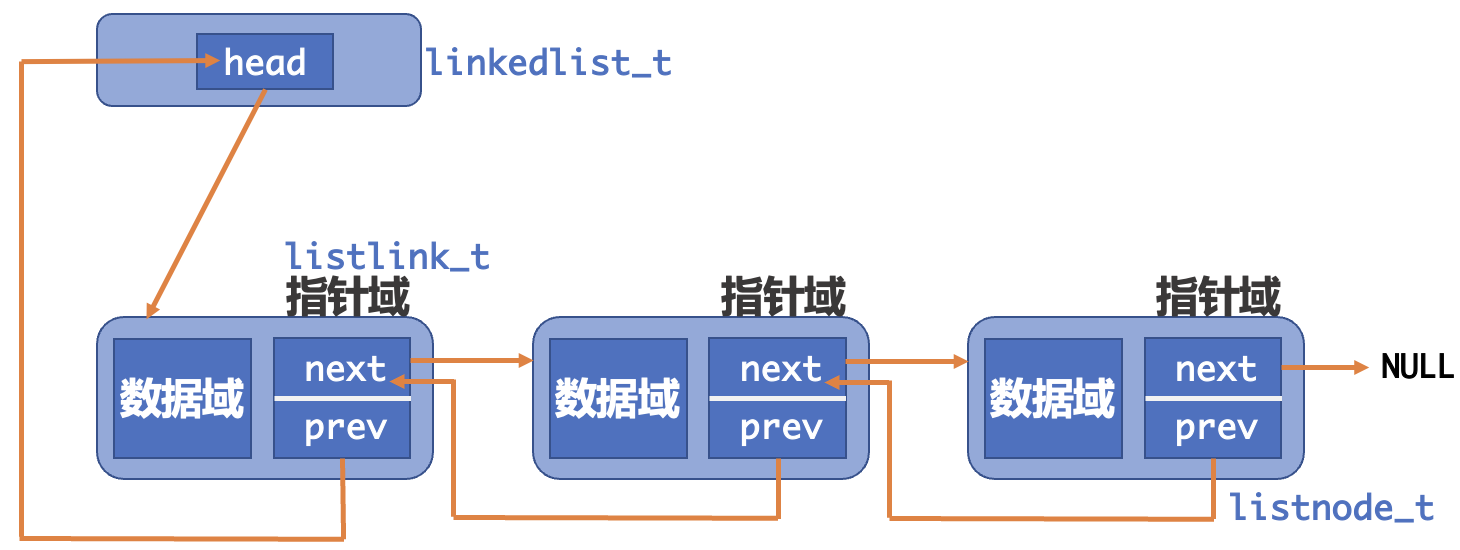
• 有一个名为linkedlist_t的结构体，这是链表的类型，其中包含了头节点的指针和其他必要信息，用这个类型定义出的每一个变量即为一个链表对象。
• 链表的每一个节点是名为listnode_t的结构体，其中包含了数据域和指针域。
• 节点中的指针域是名为listlink_t的结构体，其中有两个成员next和prev。next是listnode_t的一级指针，指向下一个节点；prev是listnode_t的二级指针，指向上一个节点的next指针。

如此封装双向链表的好处就在于把数据和链表的操作分离。假设我们规定节点中的数据域的类型永远是listdata_t类型，每次使用时，把我们需要的数据都封装进一个结构体并命名为listdata_t，则我们可以一直复用先前写好的、用于链表操作的函数。这是因为，如同前文所述，链表的所有逻辑组成，就是其指针之间的相互引用关系，而非节点中存放的数据，所以，我们把指针域专门提取出来并进行封装。

面向对象的数据结构 —— 链表篇

新类型的声明

typedef struct node listnode_t;  // 这里我们先做一个前向声明，防止后续出现无法解析类型的问题
                                 // listnode_t 即为链表的节点类型

typedef struct {
    struct node *next;           // 指向下一个节点的指针
    struct node **prev;          // 指向上一个节点的 next 的指针
} listlink_t;                    // listlink_t 是指针域类型

struct node {                    // 链表的节点
    listdata_t data;             // 数据域 —— 不用关心
    listlink_t link;             // 指针域
};

typedef struct {
    listnode_t *head;            // 链表头指针
    listnode_t *tail;            // 链表尾指针
    size_t size;                 // 链表的节点数
    
    // 当然可以有更多，如最后一次修改时间、链表的创建者等
    
} linkedlist_t;                  // linkedlist_t 即为链表类型，类比上次的 array_t

链表的初始化和销毁

assert的使用

assert即为“断言”，使用时，应该包含头文件<assert.h>。assert有一个参数，是一个条件表达式，例如assert(a != b);，这条语句的含义是“断言a不等于b”—— 假设a真的不等于b，断言成立，无事发生；假设a等于b，则断言不成立，代价是程序直接崩溃。所以我们书写的链表操作函数，传入链表类型的指针list，可以先**断言list不是NULL**。如果传入了空指针，程序直接崩溃，避免后续的麻烦。

另，以下代码注释中的调用方式全部在main中，并且假设在main的开头已经定义了linkedlist_t list;，即一个名为list、类型为linkedlist_t的链表对象。

void list_init(linkedlist_t *list)
{
    /* === 初始化链表`list` ===
       调用方式：list_init(&list);
    */
    assert(list != NULL); // 断言传入了一个非空的参数
    list->head = NULL;    // 初始化链表头节点为空
    list->tail = NULL;    // 初始化链表尾节点为空
    list->size = 0;       // 初始化链表长度为 0
}

void list_destroy(linkedlist_t *list)
{
    /* === 销毁链表`list` ===
       调用方式：list_destroy(&list);
    */
    assert(list != NULL);
    if (list->head != NULL) {  // 如果链表中有节点，则递归删除每一个节点
        list_recursive_free(list->head);
    }
    list->head = NULL;  // 重置链表头节点为空
    list->tail = NULL;  // 重置链表尾节点为空
    list->size = -1;    // 重置链表长度为无效值 -1
}
void list_recursive_free(listnode_t *node)
{
    /* === 递归删除链表节点 ===
       由 list_destroy 函数自动调用
       原理见本文第一部分
    */
    if (node->link.next != NULL) {
        list_recursive_free(node->link.next);
    }
    free(node);
}

链表的头插和尾插

我们可能需要一个函数来创建新节点，把数据域的指针传入这个函数，即可返回一个新节点

listnode_t *list_newnode(listdata_t *pdata) 
{
 /* === 创建并返回一个新节点，数据由`pdata`指明 ===
    调用方式：
       listdata_t data = {1, 3.14, 'c', "hello"}; // 假设这是数据域
       listnode_t *node = list_newnode(&data);    // p 为指向新节点的指针
 */
 listnode_t *node = (listnode_t*)malloc(sizeof(listnode_t));
                                       // 申请新节点的内存空间
 assert(node != NULL);  // 断言 malloc 成功(node 非空)
 node->data = *pdata;   // 数据赋值(结构体可以直接用等号赋值)
 node->link.prev = node->link.next = NULL; // prev 和 next 初始化为空
                    // 注意 prev 和 next 是 node 的成员 link 的成员
 return node;       // 返回新节点的指针
}

void list_insert_tail(linkedlist_t *list, listnode_t *node)
{
    /* === 在链表`list`尾插入节点`node` ===
       (本函数可以实现链栈/队的压栈/入队)
       调用方式：list_insert_tail(&list, list_newnode(&data));
    */
    assert(list != NULL);
    if (list->tail != NULL) {            // 如果尾节点存在(即链表非空)
        list->tail->link.next = node;    // 【原来尾节点】的 next 指向 node 节点
        node->link.prev = &(list->tail->link.next);
                      // 把【原来尾节点】的 next 的地址交给 node 节点的 prev 成员
    } else {                             // 如果尾节点不存在(即链表为空)
        list->head = node;               // 头节点指针指向 node
        node->link.prev = &(list->head); 
                              // 把【头节点指针】的地址交给 node 节点的 prev 成员
    }
    list->tail = node;  // 更新尾节点
    list->size++;       // 更新节点数
}

void list_insert_head(linkedlist_t *list, listnode_t *node)
{
    /* === 在链表`list`头插入节点`node` ===
       (本函数可以实现链队的出队)
       调用方式：list_insert_head(&list, list_newnode(&data));
    */
    assert(list != NULL);
    if (list->head != NULL) {          // 如果头节点存在(即链表非空)
        node->link.next = list->head;  // 新节点 node 的 next 指向【原头节点】
        list->head->link.prev = &(node->link.next);
                      // 【原头节点】的 prev 存放新节点 node 的 next 成员的地址
    } else {                // 如果头节点不存在(即链表为空)
        list->tail = node;  // 维护尾节点(因为在此之前尾节点为 NULL)
    }
    node->link.prev = &(list->head); // 把【头节点指针】的地址交给 node 节点的 prev 成员
    list->head = node;               // 更新头节点指针
    list->size++;                    // 更新节点数
}

节点的删除

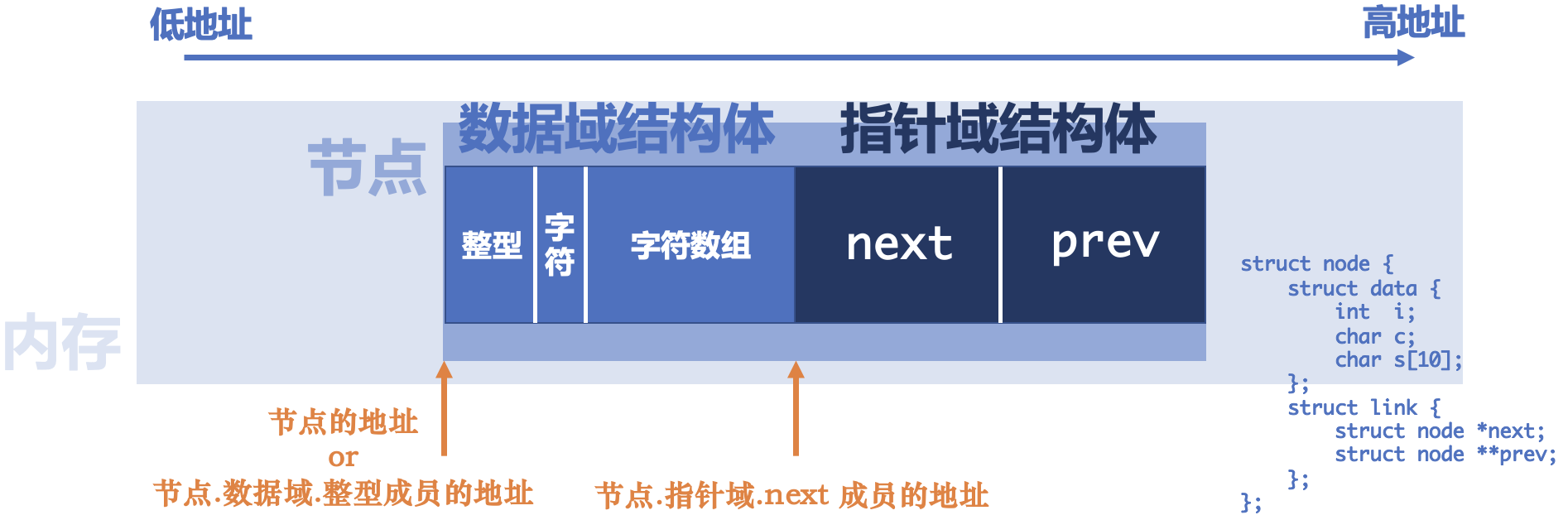
链表的删除，需要知道前一个节点的指针，在单向链表中，这个操作需要遍历链表才能实现。在我们的双向链表中，我们可以通过prev成员访问到前一个节点的next成员，这是因为prev存放的正是前一个节点next成员的地址，从而很方便地修改其值。但是，考虑这样一种情况，如果我们删除的是尾节点，固然可以通过原来尾节点的prev访问到其前一个节点的next成员并将其置为NULL，然而我们还有一个链表尾指针list->tail需要维护，我们似乎并不能通过前一个节点的next成员的地址，获取前一个节点的地址……怎么办呢？

根据此图，我们看出，结构体内部成员按照我们声明的顺序连续存放，假如我们知道了next成员的地址，减去一个“偏移量”，就可以得到节点的首地址。很自然地会想到，这个偏移量或许是sizeof(struct data)或sizeof(int) + sizeof(char) * 11。但不幸的是，为了实现结构体的字节对齐 ，结构体的各个成员之间可能会被安排一些不用于存放数据的“空洞”，所以，单纯采用sizeof获取偏移量的方法是不可行的。

不过，只要各个结构体的形态一经声明，从节点首地址到next成员地址的这一段“差值”，必然固定，所以我们只需要直接通过指针值的相减，不就能得出偏移了多少个字节吗？不过，在进行指针相减的时候，我们应先把指针都转化为void*类型，才能做到真正的整数值相减；否则，有类型的指针做减法，得到的是“相差多少个该类型的元素”。

直接给出偏移量的计算方法：(size_t) & (((listnode_t*)(0))->link.next)。

• 我们知道，NULL即为保存着地址值0的指针，也称为空指针。既然是指针，我们可以将其强转为节点指针的类型，即((listnode_t*)(0))表示的含义。这一步强转，我们手中也就获取了一个从 0 地址开始往后存放的节点结构体，虽然这个结构体并不真实存在。
• 通过指针访问成员，对应(((listnode_t*)(0))->link.next)，这个表达式即为其next成员。
• 这个“虚拟结构体”地址从 0 开始，则它的next成员的地址值，不正是“节点的next成员到节点首地址的偏移量”吗？所以我们取其地址，对应& (((listnode_t*)(0))->link.next)这个表达式。
• 最后，我们把这个偏移量强转为无符号长整型size_t。

void list_rmnode(linkedlist_t *list, listnode_t *node)
{
    /* === 删除链表`list`中的节点`node` ===
       (如果 node 参数取 list->tail，可以实现链栈的弹栈)
       调用方式：
          // 通过某种方式得到了想要删除的节点 p
          list_rmnode(&list, p);
    */
    assert(list != NULL);
    
    if (node == list->tail) { // 假设要删除链表尾节点，则需要考虑维护 tail 指针的问题
        const size_t OFFSET_OF_NEXT = (size_t) & (((listnode_t*)(0))->link.next);
            // 根据上文所述，定义一个无符号长整型的常量(也可以写成宏)
            // 这个常量用来表示【节点的 next 成员的地址】和【节点的地址】间的差值(偏移量offset)
        list->tail = (listnode_t*)((void*)(node->link.prev) - OFFSET_OF_NEXT);
            // 维护尾节点指针
            // node->link.prev 是【原尾节点的前一个节点】的【next成员】的【地址】
            // (void*)(node->link.prev) 是使之进行整数减法运算
            // 减去偏移量得到【原尾节点的前一个节点】的【地址】的数值
            // 将这一地址的整数值强转成【节点指针listnode_t*】类型，交给list->tail
    }
    
    // --- 以下是任何情况下删节点都要做的操作 ---
    
    *(node->link.prev) = node->link.next;  // 前一个节点的 next 指向要删除节点的下一个节点
    if (node->link.next != NULL) {         // 如果要删除节点后还有节点(即要删的不是尾节点)
        *((node->link.next)->link.prev) = node->link.prev;
                                           // 后面那个节点的 prev 指向前面那个节点的 next
    }
    list->size--; // 更新节点个数
    free(node);   // 最后才释放内存空间
}

当然，为了实现更完整的功能，你还需要编写更多函数。

宏的常见用法

宏（macro）可以简化代码，并且减少硬编码的成分。关于硬编码的危害，这里不再赘述了。

宏的名称应该全部大写，多个单词间用下划线分隔。

这一部分我们仅列举使用方法，不再添加解释性的内容。

程序中频繁使用的常量的定义

#define MAX_LEN 1024
#define EDGE_NUM 200
#define VERTEX_NUM 100

// 对于 4.2 题括号匹配，你可能需要
#define LEFT_PARENTHESES   '('
#define RIGHT_PARENTHESES  ')'
#define LEFT_BRACE  '{'
#define RIGHT_BRACE '}'
#define D_QUOTE '\"' // D for double
#define S_QUOTE '\'  // S for single
// 用一些整型常数定义程序当前状态，为 flag 赋值
#define NORMAL 0
#define IN_QUOTE 1
#define IN_COMMENT 2

定义小函数

#define IS_ALPHA(x) ('A' <= (x) && (x) <= 'Z' || 'a' <= (x) && (x) <= 'z')
#define IS_ALNUM(x) (IS_ALPHA(x) || '0' <= (x) && (x) <= '9')
      // 后续定义的宏可以用到已经定义过的宏
      // ctype.h 的这些函数名都是小写的，可见它们并不是用简单的宏定义的

// *** 宏的参数必须全部用括号括起来，否则会出现优先级问题
#define SQUARE_1(x) (x * x)     // 错误
#define SQUARE_2(x) ((x) * (x)) // 正确
// printf("%d\n", SQUARE_1(5 + 5)); 会被解析成
// printf("%d\n", 5 + 5 * 5 + 5);
// printf("%d\n", SQUARE_2(5 + 5)); 会被解析成
// printf("%d\n", (5 + 5) * (5 + 5));

定义复杂输出格式等

#define OUTPUT(x1, y1, x2, y2, x3, y3)                 \
			printf("A(%d, %d) B(%d, %d), C(%d, %d)",    \
			(x1), (y1), (x2), (y2), (x3), (y3))
// 分多行写则行末加上反斜杠表示连接

用宏定义功能模块

// 定义一个函数，开辟一个类型为`type`大小为`size`的数组，交给指针`p`
// 并且将这片内存都初始化为 0
#include <stdlib.h>
#include <string.h>
#define ALLOC_AND_INIT(p, type, size) do {            \
       (p) = ((type)*)malloc(sizeof(type) * (size));  \
       memset(p, 0, sizeof(type) * (size));           \
   } while(0)
// 语句外套上无用的 do-while(0) 是为了在一些特殊情况防止分号的冲突

Author: Riccardo, diandian